114.二叉树展开为链表

题目

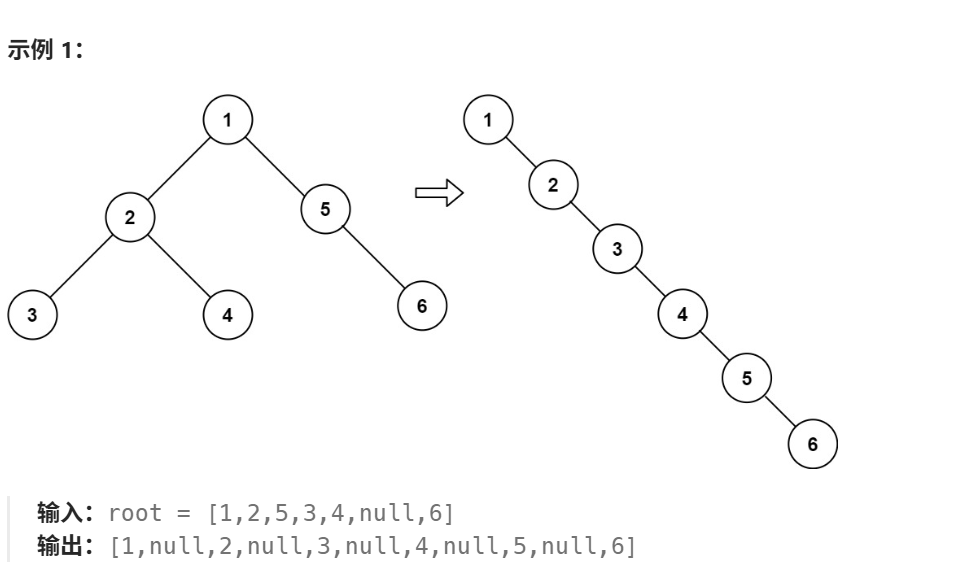
给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

思路

实现思路

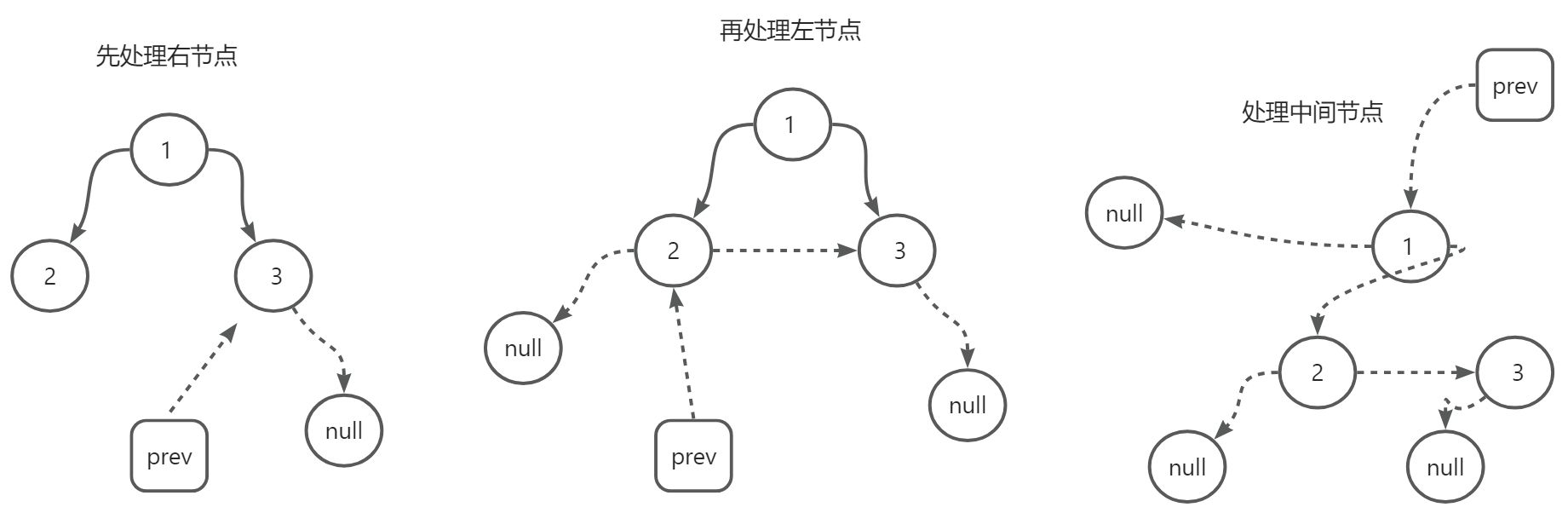
采用后序递归遍历的方式（先处理右子树，再处理左子树，最后处理当前节点），通过一个全局变量 prev 记录上一个处理完毕的节点，逐步调整指针关系。

关键步骤解析

1. 递归终止条件：若当前节点 root 为 null，直接返回（空树无需处理）。
2. 递归处理右子树：flatten(root.right)，确保右子树先被展开为单链表，prev 会记录右子树展开后的头节点。
3. 递归处理左子树：flatten(root.left)，在右子树处理完后，再展开左子树，prev 会更新为左子树展开后的头节点。
4. 调整当前节点指针：
   • 将当前节点的右指针指向 prev（即左子树展开后的头节点，若左子树为空则指向右子树展开后的头节点）；
   • 将当前节点的左指针设为 null（符合单链表要求）；
   • 更新 prev 为当前节点（供父节点处理时使用）。

假设二叉树为：

    1
   / \ 
  2   5
 / \   \
3   4   6

前序遍历为 1→2→3→4→5→6，展开后单链表为：

1.right=2 → 2.right=3 → 3.right=4 → 4.right=5 → 5.right=6 → 6.right=null，所有节点左指针均为 null。

代码

public class P114 {

    private TreeNode prev=null; // 保留处理好的节点
    public void flatten(TreeNode root) {
        if(root==null) return;
        flatten(root.right);  // 先处理右边
        flatten(root.left);   // 处理左边

        root.right=prev;
        root.left=null;
        prev=root;
    }

}

总结

复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树的节点数，每个节点仅被访问一次。
• 空间复杂度：O(h)，其中 h 是二叉树的高度，递归调用栈的深度取决于树的高度（最坏情况为链状树，h=n）。

核心特点

通过后序遍历的 “回溯” 特性，从叶子节点向根节点逐步调整指针，无需额外空间存储前序序列，实现了原地（in-place）转换。